Start from finite mixture model...

Traditional representation:

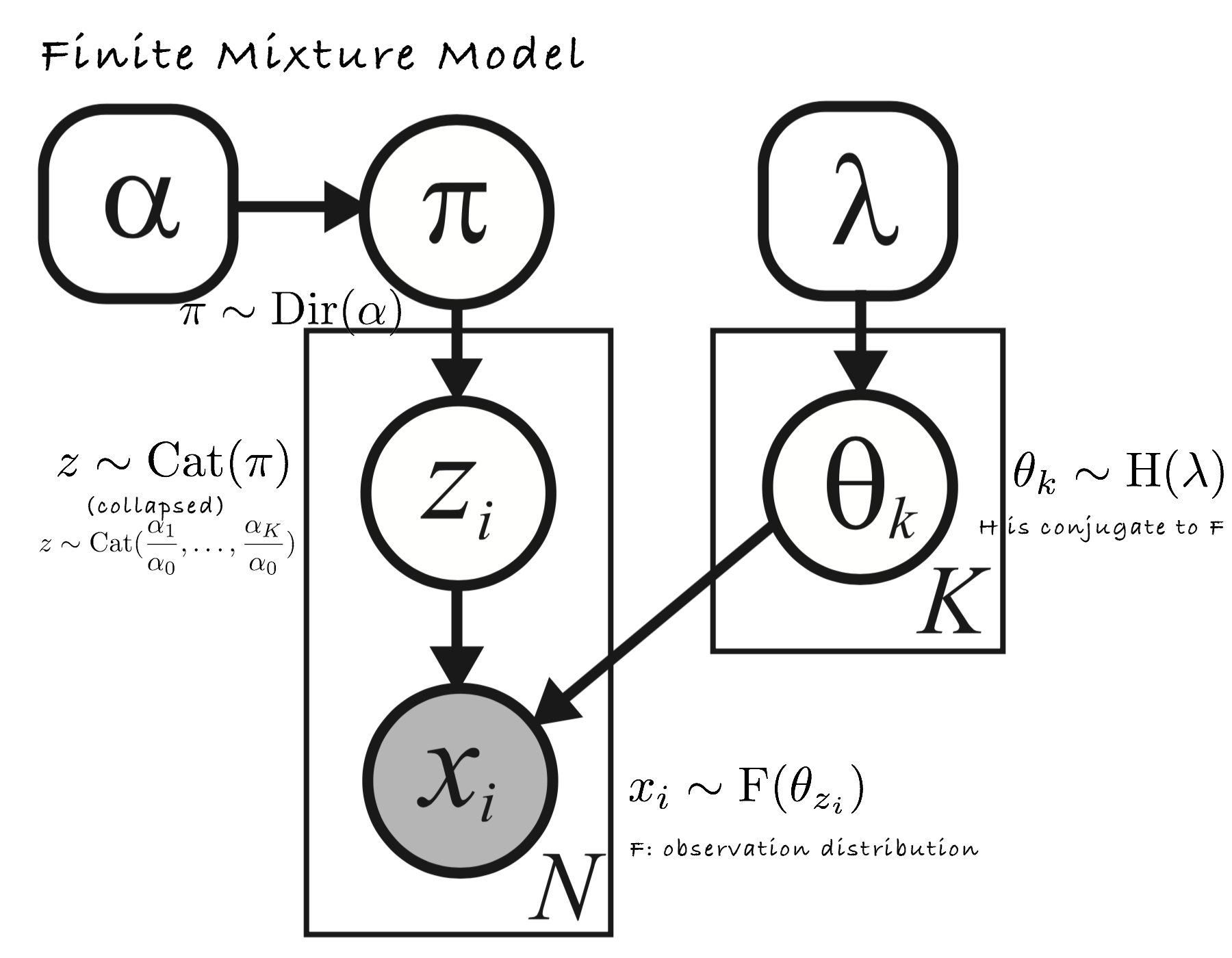
Another representation (in which H and F are both Gaussian):

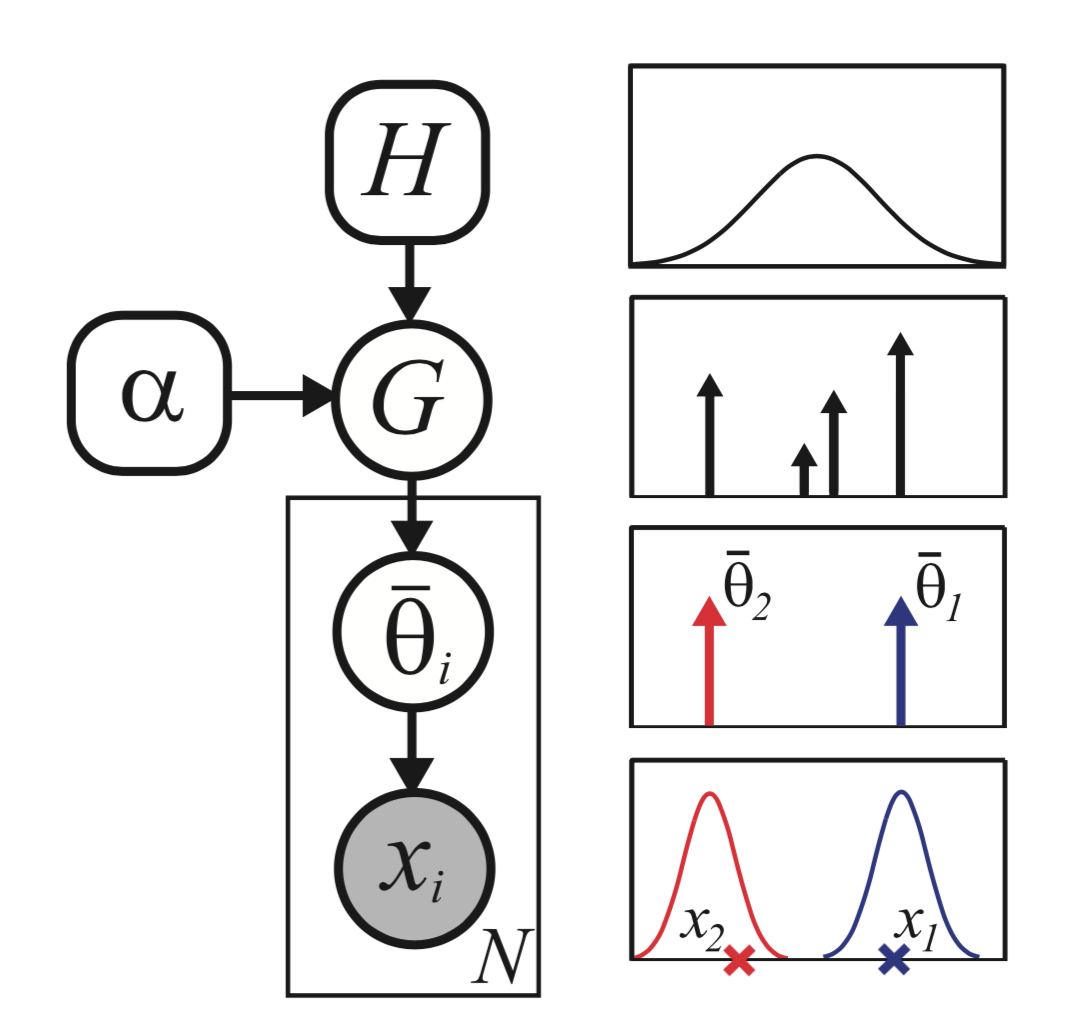
where parameters are sample from G, a discrete measure of

H $H$ :

G (θ) = \sum k = 1 K π k δ θ k (θ)

$G(\theta)=\sum_{k=1}^K\pi_k\delta_{\theta_k}(\theta)$
and

xi∼F(θ¯i) $x_i\sim \operatorname{F}(\bar \theta_i)$ .

DPMM

π∼GEM(α) $\pi\sim\operatorname{GEM}(\alpha)$ is the stick-breaking construction:

β k π k = Beta (1, α) = β k (1 - \sum l = 1 k - 1 π l)

$\begin{align} \beta_k&{}=\operatorname{Beta}(1,\alpha)\\ \pi_k&{}=\beta_k(1-\sum_{l=1}^{k-1}\pi_l) \end{align}$

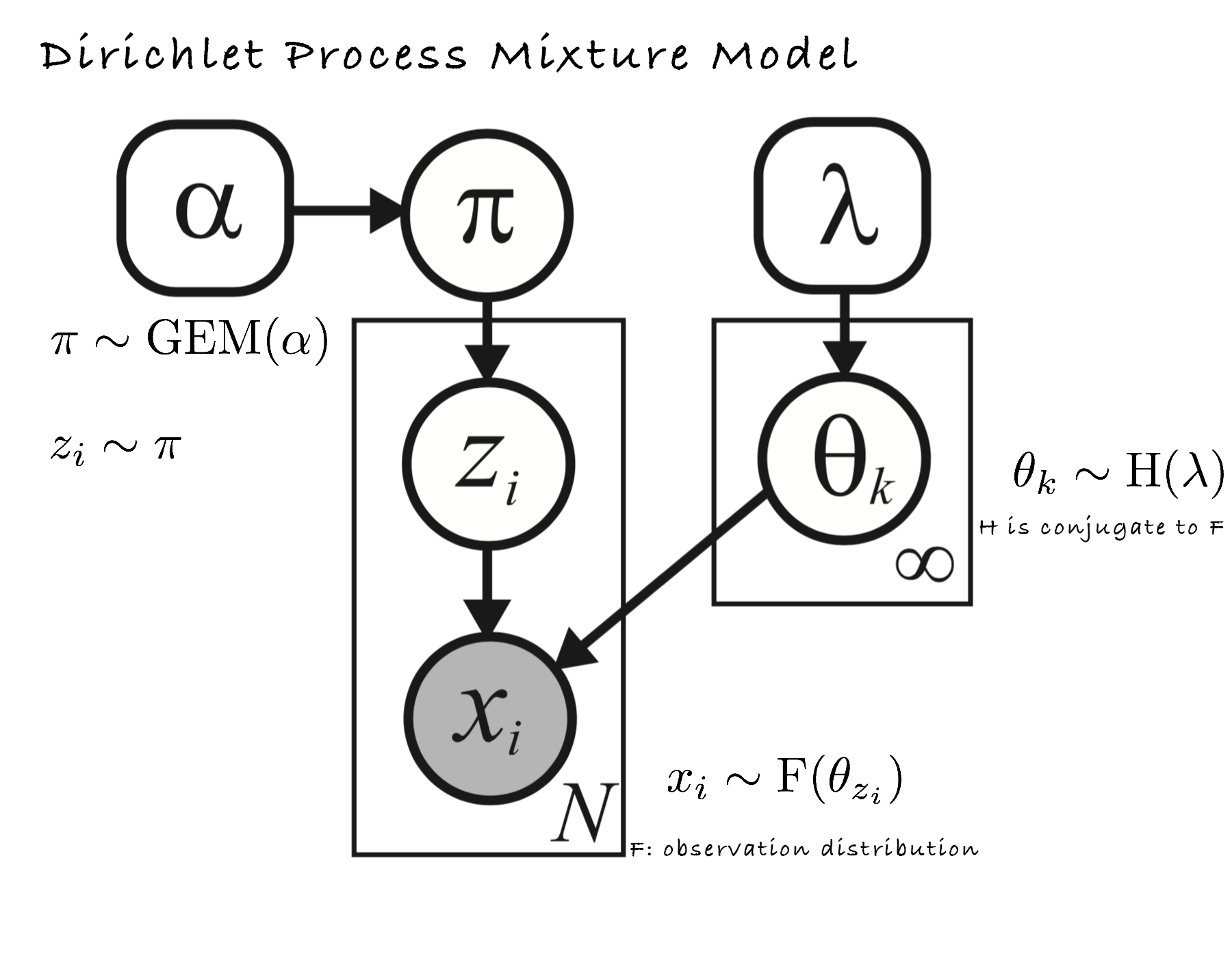
Another representation:

Where

G $G$ is a random measure

G∼DP(α,H) $G\sim\operatorname{DP}(\alpha,H)$ :

G (θ) = \sum k = 1 \infty π k δ θ k (θ)

$G(\theta)=\sum_{k=1}^\infty\pi_k\delta_{\theta_k}(\theta)$
One can show that the GEM process will terminate with probability 1, which means samples from a DP are discrete with probability 1. As

N→∞ $N\to\infty$ ,

K→αlog(N) $K\to\alpha\log(N)$ , showing that the model complexity will indeed grow logarithmically with dataset size.

model fitting (Gibbs sampling)

p (z i = k | z - i, x, α, λ) \propto p (z i = k | z - i, α) p (x i | x - i, k, λ)

$p(z_i=k| z_{-i},x,\alpha,\lambda)\propto p(z_i=k| z_{-i},\alpha)\ p(x_i| x_{- i,k},\lambda)$

p (z i = k | z - i, α) = {N k , - i α + N - 1 α α + N - 1 if k has been seen before if k is a new cluster

$p(z_i=k| z_{- i},\alpha)= \begin{cases} \frac{N_{k,-i}}{\alpha+N-1} &\text{if k has been seen before}\\ \frac{\alpha}{\alpha+N-1} &\text{if k is a new cluster} \end{cases}$

p (x i | x - i, k, λ) = p ( x i , x - i , k | λ ) p ( x - i , k | λ )

$p(x_i| x_{- i,k},\lambda)=\frac{p(x_i, x_{- i,k}|\lambda)}{p( x_{- i,k}|\lambda)}$
where

p(xi,x−i,k|λ) $p(x_i, x_{- i,k}|\lambda)$ is the marginal likelihood of all the data assigned to cluster

k $k$ , including

i $i$ , and

p(x−i,k|λ) $p(x_{−i,k}|\lambda)$ is an analogous expression excluding

i $i$ .

Example: DPMM algorithm for clustering:

Random initial assignment to clusters
loop
  unassign an observation
  choose new cluster for that observation
until convergence

Gibbs sampling for choosing cluster:

p (z i = k ∣ ∣ z - i, x, α) = ⎧ ⎩ ⎨ ⎪ ⎪ (N k N + α)  (x, N k x ¯ N k + 1, 1) α N + α  (x, 0, 1) existing cluster k new cluster

$p(\left.z_i=k\right|z_{-i},x,\alpha)= \begin{cases} \left(\frac{N_k}{N+\alpha}\right)\mathcal N\left(x,\frac{N_k\bar x}{N_k+1},1\right)&\text{existing cluster k}\\ \frac{\alpha}{N+\alpha}\mathcal N(x,0,1) &\text{new cluster} \end{cases}$
on the assumption that base distribution G is normal distribution with zero mean and unit variance.

(x,μ,Σ) $\mathcal N(x,\mu,\Sigma)$ is the probability of generate

x $x$ from a Gaussian with mean

μ $\mu$ and variance

Σ $\Sigma$ .

Reference

"Machine Learning" Lecture 17: http://www.umiacs.umd.edu/~jbg/teaching/CSCI_5622/
Book: Machine Learning - A Probabilistic Perspective(Chapter 25)

Dirichlet Process Mixture Model

Start from finite mixture model...

DPMM

model fitting (Gibbs sampling)

Example: DPMM algorithm for clustering:

Reference